542. 01 Matrix (M)

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

Example 1:

Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

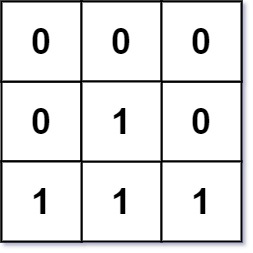
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

Constraints:

• m == mat.length

• n == mat[i].length

• 1 <= m, n <= 104

• 1 <= m * n <= 104

• mat[i][j] is either 0 or 1.

• There is at least one 0 in mat.

Solution:

https://www.jiuzhang.com/problem/01-matrix/

Version 1: BFS

先把所有的0 进queue， 再一个一个pop

class Solution {
    private int[][] result;
    public int[][] updateMatrix(int[][] mat) {
        
        int m = mat.length;
        int n = mat[0].length;
        int[][] result = new int[m][n];
        boolean[][] visited = new boolean[m][n];
        Queue<Node> queue = new LinkedList<Node>();
        
        int[] dx = new int[]{-1,1,0,0};
        int[] dy = new int[]{0,0,-1,1};
        for(int i = 0; i< m; i++)
        {
            for(int j = 0; j< n; j++)
            {
                if(mat[i][j] == 0)
                {
                    visited[i][j] = true;
                    queue.offer(new Node(i,j));
                    
                    result[i][j] = 0;
                }else
                {
                    result[i][j] = Integer.MAX_VALUE;
                }
            }
        }
        
        while(! queue.isEmpty())
        {
            int size = queue.size();
            for(int i = 0;i< size;i++)
            {
                Node current = queue.poll();
                for(int k = 0; k< 4; k++)
                {
                    int directX = current.x + dx[k];
                    int directY = current.y + dy[k];
                    if(isBound(mat, directX, directY) && !visited[directX][directY])
                    {
                        queue.offer(new Node(directX, directY));
                        visited[directX][directY] = true;
                        result[directX][directY] = Math.min(result[directX][directY], result[current.x][current.y] + 1);
                    }
                }
            }
        }
        return result;
    }
    
    
    public boolean isBound(int[][] mat, int x, int y)
    {
        int m = mat.length;
        int n = mat[0].length;
        return x>=0 & x<m && y >=0 && y<n;
    }
}

class Node
{
    int x;
    int y;
    Node(int x, int y)
    {
        this.x = x;
        this.y = y;
        
    }
}

Version 2: DP

从左上出发推一遍。 从右下出发推一遍。

public class Solution {
    /**
     * @param matrix: a 0-1 matrix
     * @return: return a matrix
     */
    public int[][] updateMatrix(int[][] matrix) {
        // write your code here
        int n = matrix.length, m = matrix[0].length;
        int[][] dp = new int[n][m];
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if (matrix[i][j] == 0) dp[i][j] = 0;
                //注意这里不要给MAX_VALUE不要会溢出。test case 见下
                else dp[i][j] = 1000000;
                if (i > 0) dp[i][j] = Math.min(dp[i][j], dp[i - 1][j] + 1);
                if (j > 0) dp[i][j] = Math.min(dp[i][j], dp[i][j - 1] + 1);
            }
        }
        for (int i = n - 1; i >= 0; --i) {
            for (int j = m - 1; j >= 0; --j) {
                if (dp[i][j] > 0) {
                    if (i < n - 1) dp[i][j] = Math.min(dp[i][j], dp[i + 1][j] + 1);
                    if (j < m - 1) dp[i][j] = Math.min(dp[i][j], dp[i][j + 1] + 1);
                }
            }
        }
        return dp;
    }
}

test case:

Input: [[1,0,1,1,0,0,1,0,0,1],[0,1,1,0,1,0,1,0,1,1],[0,0,1,0,1,0,0,1,0,0],[1,0,1,0,1,1,1,1,1,1],[0,1,0,1,1,0,0,0,0,1],[0,0,1,0,1,1,1,0,1,0],[0,1,0,1,0,1,0,0,1,1],[1,0,0,0,1,1,1,1,0,1],[1,1,1,1,1,1,1,0,1,0],[1,1,1,1,0,1,0,0,1,1]]

Output: [[-2147483647,-2147483648,-2147483647,-2147483646,-2147483645,-2147483644,-2147483643,-2147483642,-2147483641,-2147483640],[-2147483648,-2147483647,-2147483646,-2147483645,-2147483644,-2147483643,-2147483642,-2147483641,-2147483640,-2147483639],[-2147483647,-2147483646,-2147483645,-2147483644,-2147483643,-2147483642,-2147483641,-2147483640,-2147483639,-2147483638],[-2147483646,-2147483645,-2147483644,-2147483643,-2147483642,-2147483641,-2147483640,-2147483639,-2147483638,-2147483637],[-2147483645,-2147483644,-2147483643,-2147483642,-2147483641,-2147483640,-2147483639,-2147483638,-2147483637,-2147483636],[-2147483644,-2147483643,-2147483642,-2147483641,-2147483640,-2147483639,-2147483638,-2147483637,-2147483636,-2147483635],[-2147483643,-2147483642,-2147483641,-2147483640,-2147483639,-2147483638,-2147483637,-2147483636,-2147483635,-2147483634],[-2147483642,-2147483641,-2147483640,-2147483639,-2147483638,-2147483637,-2147483636,-2147483635,-2147483634,-2147483633],[-2147483641,-2147483640,-2147483639,-2147483638,-2147483637,-2147483636,-2147483635,-2147483634,-2147483633,-2147483632],[-2147483640,-2147483639,-2147483638,-2147483637,-2147483636,-2147483635,-2147483634,-2147483633,-2147483632,-2147483631]]

Expected: [[1,0,1,1,0,0,1,0,0,1],[0,1,1,0,1,0,1,0,1,1],[0,0,1,0,1,0,0,1,0,0],[1,0,1,0,1,1,1,1,1,1],[0,1,0,1,1,0,0,0,0,1],[0,0,1,0,1,1,1,0,1,0],[0,1,0,1,0,1,0,0,1,1],[1,0,0,0,1,2,1,1,0,1],[2,1,1,1,1,2,1,0,1,0],[3,2,2,1,0,1,0,0,1,1]]