95. Unique Binary Search Trees II (M)

https://leetcode.com/problems/unique-binary-search-trees-ii/

Given an integer n, return all the structurally unique BST's (binary search trees), which has exactly n nodes of unique values from 1 to n. Return the answer in any order.

Example 1:

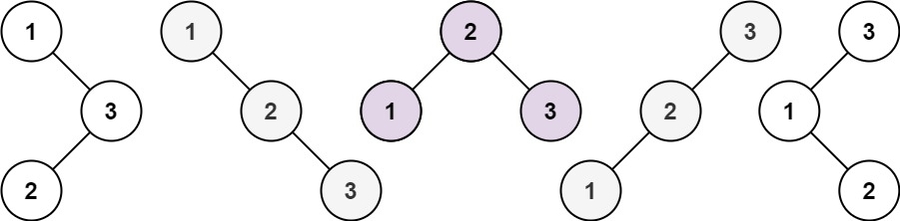
Input: n = 3
Output: [[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

Example 2:

Input: n = 1
Output: [[1]]

Constraints:

• 1 <= n <= 8

Solution:

https://www.jiuzhang.com/problem/unique-binary-search-trees-ii/

明白了上道题构造合法 BST 的方法，这道题的思路也是一样的：

1、穷举root节点的所有可能。

2、递归构造出左右子树的所有合法 BST。

3、给root节点穷举所有左右子树的组合。

由于二叉查找树的性质，对于一个二叉查找树的节点，它的左子树中所有节点的值都小于它的值，它的右子树中所有节点的值都大于它的值。而且二叉查找树的中序遍历是一个排好序的数组。

我们可以枚举根节点的所有可能的值。如果根节点的值等于ii，那么左子树的节点值在范围1,i−1内，右子树节点的值在范围i+1,n中。遍历左子树的所有情况和右子树的所有情况，就可以组合出当根节点的值等于ii时的所有情况。

根据以上的推导，我们可以发现这是一个明显的递归结构，左右子树也可以用这个递归结构构造。那么我们就可以用递归来解决这个问题。

代码思路

递归的步骤：

1、递归出口，如果start值大于end值，返回一个只含空节点的列表。

2、枚举根节点的值root_val，从start到end。

3、递归获得所有可能的左子树start, root_val - 1。

4、递归获得所有可能的右子树root_val + 1, end。

5、遍历左右子树的所有可能，组合成新的树，加入结果数组result中。

6、返回结果数组result。

复杂度分析

设二叉查找树的节点数为NN。 C(n)=(2n)!/(n!(n+1)!)为卡特兰数第n项的计算公式。 所有不同的节点数为NN的二叉查找树为对应的卡特兰数C(N)。

时间复杂度：O(N∗C(N))

由于有的子树会被重复计算，时间复杂度为O(N∗C(N))。

空间复杂度：O(N)

空间复杂度取决于树的最大深度，O(N)。

源代码

javapythonc++

/**
 * Definition of TreeNode:
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left, right;
 *     public TreeNode(int val) {
 *         this.val = val;
 *         this.left = this.right = null;
 *     }
 * }
 */
public class Solution {
    /**
     * @paramn n: An integer
     * @return: A list of root
     */
    public List<TreeNode> generateTrees(int n) {
        return helper(1, n);
    }
    // 返回值是从start到end的所有可能的二叉查找树
    public List<TreeNode> helper(int start, int end) {
        List<TreeNode> result = new ArrayList<>();

        // 递归出口
        if (start > end) {
            result.add(null);
            return result;
        }
        
        // 枚举根节点的值
        for (int rootVal = start; rootVal <= end; rootVal++) {
            // 递归获得所有可能的左子树
            List<TreeNode> leftTrees = helper(start, rootVal - 1);
            // 递归获得所有可能的右子树
            List<TreeNode> rightTrees = helper(rootVal + 1, end);
            // 枚举每一种左右子树的组合，组成新的二叉树
            for (int i = 0; i < leftTrees.size(); i++) {
                TreeNode leftTree = leftTrees.get(i);
                for (int j = 0; j < rightTrees.size(); j++) {
                    TreeNode rightTree = rightTrees.get(j);
                    TreeNode root = new TreeNode(rootVal);
                    root.left = leftTree;
                    root.right = rightTree;
                    result.add(root);
                }
            }
        }
        return result;
    }
}