240. Search a 2D Matrix II

Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.

• Integers in each column are sorted in ascending from top to bottom.

Example 1:

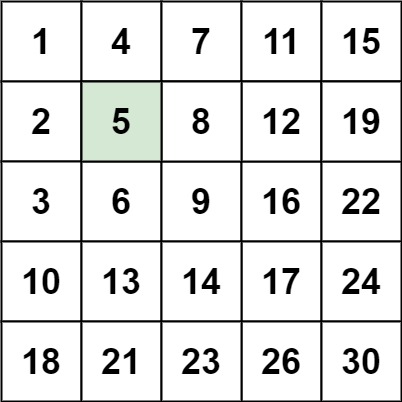
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

Example 2:

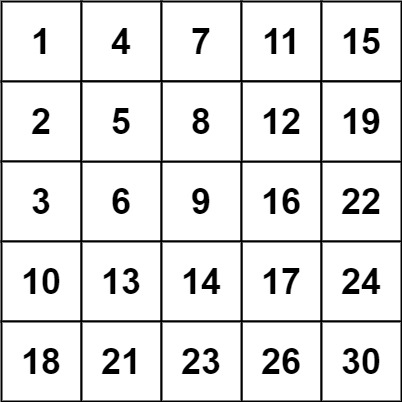
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

Constraints:

• m == matrix.length

• n == matrix[i].length

• 1 <= n, m <= 300

• -109 <= matrix[i][j] <= 109

• All the integers in each row are sorted in ascending order.

• All the integers in each column are sorted in ascending order.

• -109 <= target <= 109

Solution:

Version 1:

一定要先target到row, 再找column, 反向的话会有错.

test case

[[1,2,3,4,5],[6,7,8,9,10],[11,12,13,14,15],[16,17,18,19,20],[21,22,23,24,25]]

19

当锁定了row number之后，要在0- row之前的每一行都搜索，

[[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]]

5

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        
        int m = matrix.length;
        int n = matrix[0].length;
        
        int start = 0;
        int end = m-1;
        int firstRowIndex = 0;
        
        while(start+1 < end)
        {
            int mid = start + (end-start)/2;
            if(target == matrix[mid][0])
            {
                return true;
            }
            else if(target > matrix[mid][0])
            {
                start = mid;
            }
            else if(target < matrix[mid][0])
            {
                end = mid;
            }
        }
        
        if(matrix[end][0] <= target)
        {
            firstRowIndex = end;
        }
        else if(matrix[start][0] <= target)
        {
            firstRowIndex = start;
        }

        
        for(int i = 0; i<= firstRowIndex; i++)
        {
            start = 0;
            end = n-1;

            while(start + 1 < end)
            {
                int mid = start + (end-start)/2;
                if(target == matrix[i][mid])
                {
                    return true;
                }
                else if(target > matrix[i][mid])
                {
                    start = mid;
                }
                else if(target < matrix[i][mid])
                {
                    end = mid;
                }
            }

            if(matrix[i][end] == target)
            {
                return true;
            }
            else if(matrix[i][start] == target)
            {
                return true;
            }
        }
    
        return false;  
    }

}

Version 2:

根据题意，每行中的整数从左到右是排序的，每一列的整数从上到下是排序的，在每一行或每一列中没有重复的整数。那么我们只要从矩阵的左下角开始向右上角找，若是小于target就往右找，若是大于target就往上找

• 从左下角即(n-1,0)处出发

• 如果matrix[x][y] < target 下一步往右搜

• 如果matrix[x][y] > target 下一步往上搜

• 如果matrix[x][y] = target 下一步往[x-1][y+1]即右上角搜，因为是有序的，每一行每一列中每个数都是唯一的

复杂度分析

• 时间复杂度O(n+m)

  • 左下角往右上角呈阶梯状走，长度为n+m

• 空间复杂度O(size(matrix))

  • 地图的大小

public boolean searchMatrix(int[][] matrix, int target) {
        
        int m = matrix.length;
        int n = matrix[0].length;
        
        int x = m-1;
        int y = 0;
        
        while(x>=0 && y<n)
        {
            if(matrix[x][y] == target)
            {
                return true;
            }
            else if(matrix[x][y] > target)
            {
                x--;
            }
            else if(matrix[x][y] < target)
            {
                y++;
            }
        }
        return false;
       
    }