1584. Min Cost to Connect All Points (M)

https://leetcode.com/problems/min-cost-to-connect-all-points/

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].

The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.

Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.

Example 1:

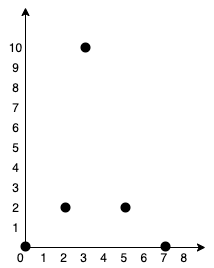
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20
Explanation: 

We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.

Example 2:

Input: points = [[3,12],[-2,5],[-4,1]]
Output: 18

Constraints:

• 1 <= points.length <= 1000

• -106 <= xi, yi <= 106

• All pairs (xi, yi) are distinct.

Solution:

很显然这也是一个标准的最小生成树问题：每个点就是无向加权图中的节点，边的权重就是曼哈顿距离，连接所有点的最小费用就是最小生成树的权重和。

所以解法思路就是先生成所有的边以及权重，然后对这些边执行 Kruskal 算法即可：

int minCostConnectPoints(int[][] points) 
{    
    int n = points.length;    
    // 生成所有边及权重    
    List<int[]> edges = new ArrayList<>();    
    for (int i = 0; i < n; i++) 
    {        
        for (int j = i + 1; j < n; j++) 
        {            
            int xi = points[i][0], yi = points[i][1];            
            int xj = points[j][0], yj = points[j][1];            
            // 用坐标点在 points 中的索引表示坐标点            
            edges.add(new int[] {i, j, Math.abs(xi - xj) + Math.abs(yi - yj) }); 
        }    
    }    
    // 将边按照权重从小到大排序    
    Collections.sort(edges, (a, b) -> {return a[2] - b[2];});    
    // 执行 Kruskal 算法    
    int mst = 0;    
    UF uf = new UF(n);    
    for (int[] edge : edges) 
    {        
        int u = edge[0];        
        int v = edge[1];        
        int weight = edge[2];        
        // 若这条边会产生环，则不能加入 mst        
        if (uf.connected(u, v)) 
        {            
            continue;        
        }        
        // 若这条边不会产生环，则属于最小生成树        
        mst += weight;        
        uf.union(u, v);    
    }    
    return mst;
}

这道题做了一个小的变通：每个坐标点是一个二元组，那么按理说应该用五元组表示一条带权重的边，但这样的话不便执行 Union-Find 算法；所以我们用 points 数组中的索引代表每个坐标点，这样就可以直接复用之前的 Kruskal 算法逻辑了。

通过以上三道算法题，相信你已经掌握了 Kruskal 算法，主要的难点是利用 Union-Find 并查集算法向最小生成树中添加边，配合排序的贪心思路，从而得到一棵权重之和最小的生成树。