二分图判定

https://labuladong.github.io/algo/2/19/36/

在讲二分图的判定算法之前，我们先来看下百度百科对「二分图」的定义：

二分图的顶点集可分割为两个互不相交的子集，图中每条边依附的两个顶点都分属于这两个子集，且两个子集内的顶点不相邻。

其实图论里面很多术语的定义都比较拗口，不容易理解。我们甭看这个死板的定义了，来玩个游戏吧：

给你一幅「图」，请你用两种颜色将图中的所有顶点着色，且使得任意一条边的两个端点的颜色都不相同，你能做到吗？

这就是图的「双色问题」，其实这个问题就等同于二分图的判定问题，如果你能够成功地将图染色，那么这幅图就是一幅二分图，反之则不是：

在具体讲解二分图判定算法之前，我们先来说说计算机大佬们闲着无聊解决双色问题的目的是什么。

首先，二分图作为一种特殊的图模型，会被很多高级图算法（比如最大流算法）用到，不过这些高级算法我们不是特别有必要去掌握，有兴趣的读者可以自行搜索。

从简单实用的角度来看，二分图结构在某些场景可以更高效地存储数据。

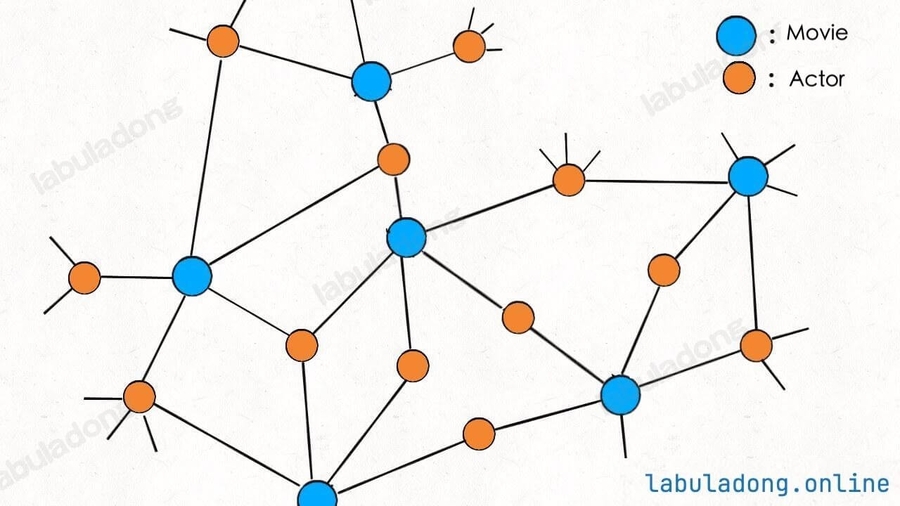
比如前文 介绍《算法 4》 文章中的例子，如何存储电影演员和电影之间的关系？

如果用哈希表存储，需要两个哈希表分别存储「每个演员到电影列表」的映射和「每部电影到演员列表」的映射。

但如果用「图」结构存储，将电影和参演的演员连接，很自然地就成为了一幅二分图：

每个电影节点的相邻节点就是参演该电影的所有演员，每个演员的相邻节点就是该演员参演过的所有电影，非常方便直观。

类比这个例子，其实生活中不少实体的关系都能自然地形成二分图结构，所以在某些场景下图结构也可以作为存储键值对的数据结构（符号表）。

好了，接下来进入正题，说说如何判定一幅图是否是二分图。

二分图判定思路

判定二分图的算法很简单，就是用代码解决「双色问题」。

说白了就是遍历一遍图，一边遍历一边染色，看看能不能用两种颜色给所有节点染色，且相邻节点的颜色都不相同。

既然说到遍历图，也不涉及最短路径之类的，当然是 DFS 算法和 BFS 皆可了，DFS 算法相对更常用些，所以我们先来看看如何用 DFS 算法判定双色图。

首先，基于 学习数据结构和算法的框架思维 写出图的遍历框架：

/* 二叉树遍历框架 */
void traverse(TreeNode root) {
    if (root == null) return;
    traverse(root.left);
    traverse(root.right);
}

/* 多叉树遍历框架 */
void traverse(Node root) {
    if (root == null) return;
    for (Node child : root.children)
        traverse(child);
}

/* 图遍历框架 */
boolean[] visited;
void traverse(Graph graph, int v) {
    // 防止走回头路进入死循环
    if (visited[v]) return;
    // 前序遍历位置，标记节点 v 已访问
    visited[v] = true;
    for (TreeNode neighbor : graph.neighbors(v))
        traverse(graph, neighbor);
}

因为图中可能存在环，所以用 visited 数组防止走回头路。

这里可以看到我习惯把 return 语句都放在函数开头，因为一般 return 语句都是 base case，集中放在一起可以让算法结构更清晰。

其实，如果你愿意，也可以把 if 判断放到其它地方，比如图遍历框架可以稍微改改：

/* 图遍历框架 */
boolean[] visited;
void traverse(Graph graph, int v) {
    // 前序遍历位置，标记节点 v 已访问
    visited[v] = true;
    for (int neighbor : graph.neighbors(v)) {
        if (!visited[neighbor]) {
            // 只遍历没标记过的相邻节点
            traverse(graph, neighbor);
        }
    }
}

这种写法把对 visited 的判断放到递归调用之前，和之前的写法唯一的不同就是，你需要保证调用 traverse(v) 的时候，visited[v] == false。

为什么要特别说这种写法呢？因为我们判断二分图的算法会用到这种写法。

回顾一下二分图怎么判断，其实就是让 traverse 函数一边遍历节点，一边给节点染色，尝试让每对相邻节点的颜色都不一样。

所以，判定二分图的代码逻辑可以这样写：

/* 图遍历框架 */
void traverse(Graph graph, boolean[] visited, int v) {
    visited[v] = true;
    // 遍历节点 v 的所有相邻节点 neighbor
    for (int neighbor : graph.neighbors(v)) {
        if (!visited[neighbor]) {
            // 相邻节点 neighbor 没有被访问过
            // 那么应该给节点 neighbor 涂上和节点 v 不同的颜色
            traverse(graph, visited, neighbor);
        } else {
            // 相邻节点 neighbor 已经被访问过
            // 那么应该比较节点 neighbor 和节点 v 的颜色
            // 若相同，则此图不是二分图
        }
    }
}

如果你能看懂上面这段代码，就能写出二分图判定的具体代码了，接下来看LeetCode 785。886